nLab round sphere

Idea

In Riemannian geometry, the topological n-sphere regarded as a Riemannian manifold in the standard way (i.e. as the submanifold of elements at constant distance from a given point in Euclidean space) is also called the round $n$-sphere, in order to distinguish it from other, non-isometric Riemannian manifold structures that also exists on some n-sphere. These alternatives are then also called squashed spheres.

Properties

Proposition

For $n \in \mathbb{N}_{\gt 0}$ and $r \in \mathbb{R}_{\gt 0}$, the Ricci tensor of the round $n$-sphere $S^n$ of radius $r$ satisfies

$$Ric(v,v) \;=\; \frac{n-1}{r^2}$$

for all unit-length tangent vectors $v \in T S^n$, ${\vert v \vert} = 1$.

Accordingly, the scalar curvature of the round $n$-sphere of radius $r$ is the constant function with value

$$\mathrm{R} \;=\; \frac{n(n-1)}{r^2} \,.$$

(e.g. Lee 2018, Cor. 11.20)

Examples of squashed $n$-spheres

coset space-structures on n-spheres:

standard:
$S^{n-1} \simeq_{diff} SO(n)/SO(n-1)$	this Prop.
$S^{2n-1} \simeq_{diff} SU(n)/SU(n-1)$	this Prop.
$S^{4n-1} \simeq_{diff} Sp(n)/Sp(n-1)$	this Prop.
exceptional:
$S^7 \simeq_{diff} Spin(7)/G_2$	Spin(7)/G₂ is the 7-sphere
$S^7 \simeq_{diff} Spin(6)/SU(3)$	since Spin(6) $\simeq$ SU(4)
$S^7 \simeq_{diff} Spin(5)/SU(2)$	since Sp(2) is Spin(5) and Sp(1) is SU(2), see Spin(5)/SU(2) is the 7-sphere
$S^6 \simeq_{diff} G_2/SU(3)$	G₂/SU(3) is the 6-sphere
$S^15 \simeq_{diff} Spin(9)/Spin(7)$	Spin(9)/Spin(7) is the 15-sphere

see also Spin(8)-subgroups and reductions

homotopy fibers of homotopy pullbacks of classifying spaces:

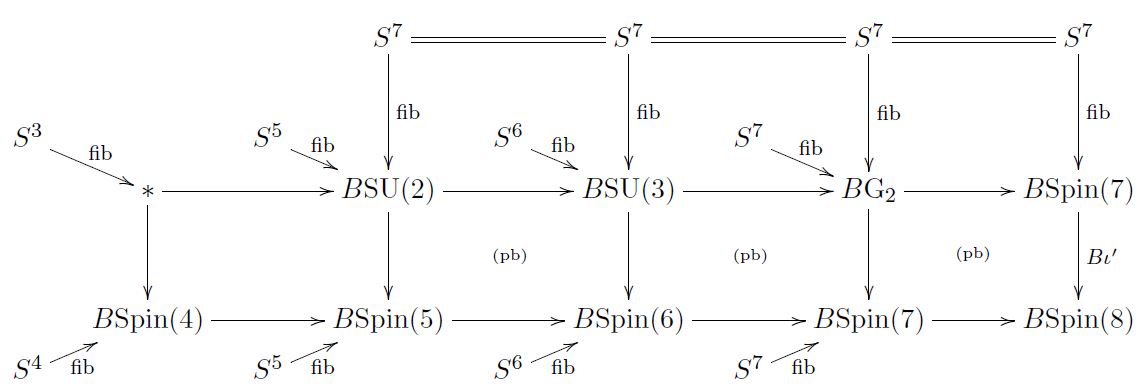
(from FSS 19, 3.4)

Related concepts

• exotic sphere

• spherical space form

• Riemann sphere